はじめまして、okashitayです。
2019年12月3日 アイスタイル Advent Calendar 2019を担当させていただきます。
はじめに
本日2019年12月3日 は弊社のサービス@cosmeが20年を迎えました。すごいですね…、移り変わりの早いWebサービスが20年も続くのって!
多くのWebサービスは時代の「流れ」をいちはやく読み、その時の「流れ」にのったとしても大抵のサービスは数年後には消えていくのが大半ではないでしょうか。
本日はそこで「流れ」に関してのテクノロジー、「流体シミュレーション」について、学びやすいように理論・数式から少し紐解いて行こうと思います。
「流れ」とは
何かの移りかわりである。
「流体」とは
気体と液体を指していて、自由に変形できるもの。
「シミュレーション」とは
対象となるシステムで働いている法則を推定・抽出し、それを真似るようにして組み込んだモデル、模型、コンピュータプログラムなどを用いて行われる。現実のシステムを動かしてその挙動や結果を確かめることが困難、不可能、または危険である場合にシミュレーションが用いられる。例えば、社会現象などにおける問題の解決方法を探る時など、(悪影響があるので実社会ではとりあえず試せないので)実際の社会と似た状況を数式などで作りだし、コンピュータ等を用いて模擬的に動かし、その特性などを把握するのに用いる。例えば風洞実験、水槽実験で働いている法則を数学的なモデルに置き換えて行う。また例えば経営に関する様々な事象を数学的なモデルに置き換えてみて、様々な数値を入力したり変化させることで、結果を推定する。(wikipediaより)
流体シミュレーションで重要な数式
ナビエ・ストークス方程式(NS方程式)
図1.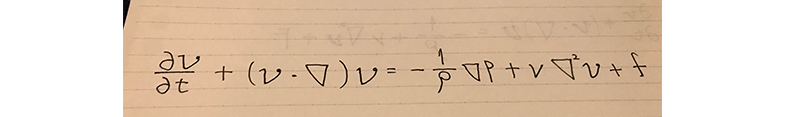
左辺 第1項:時間微分項、第2項:移流項
右辺 第1項:圧力項、第2項:粘性項(拡散項) 第3項:外力項
NS方程式の項を全て計算する事により現実の動き近づくことができます。
各種記号の意味
・ ∂:ラウンド、偏微分記号
・ v:流速(velocity) 時刻(t)における位置(x)の流体の速度、ベクトル場
・ ∇:ナブラ、 ∇の次に来る記号のベクトル場を空間微分する意味
・ V:動粘性(viscosity)係数:∇2乗の左側、粘性係数を密度で割ったもの
・ ρ:ロー、単位面積(3次元だと体積)あたりの流体の密度(density)
・ P:圧力(pressure) 時刻(t)における位置(x)の圧力
・ f:外力 単位質量あたりの外力、風や重力など
また、密度と粘性が一定のものを非圧縮性という。
(圧力を加えても密度が変わることがない、水、空気など身の回りにあるもの)
ざっと、見た感じわからないですよね…
わかりやすく考えると古典力学でいうニュートンの第2の方程式(ma=F)と同じです。
図1のNS方程式を両辺にρを掛けると
図2.
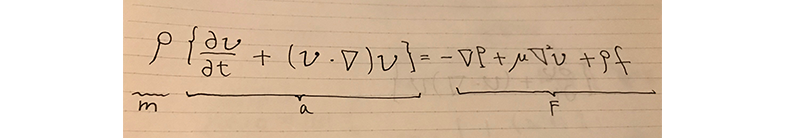
ρが質量、その隣の{}で囲んだ式が加速度そして右辺Fが力となります(粘性項は粘性係数μに変化)。運動方程式の部分、物体の質量とそれに加わる力を与えると、その物体の運動が全て予想することができます。それが流体の運動の世界ではNS方程式を解く事によってありとあらゆる、流体の運動現象が求まります。
シミュレーションする上で重要な2つの手法
・粒子法
連続体に関する方程式を数値的に解くための離散化手法の一つで、計算対象物を粒子の集まりとして表すことからこのように呼ばれる。一つ一つの粒子が物理的情報を持ち、変化を計算して動かします。それゆえに、さざ波や水しぶきなどの流体表面の細部の動きをシミュレーションできる。
・格子法
流体で扱う空間を格子で分割して、それぞれの格子に対し速度、密度などの物理情報を持ち変化を計算させて動きをシミュレーションさせます。格子上の計算を行ない値を求めること、数学的にわかりやすい。ただし形状が複雑な場合、領域に沿った形状で計算することが難しい。現実に近いものを作ろうとすると計算負荷が高い。
格子法のイメージ
図3.(Real-Time Fluid Dynamics for Gamesより抜粋) 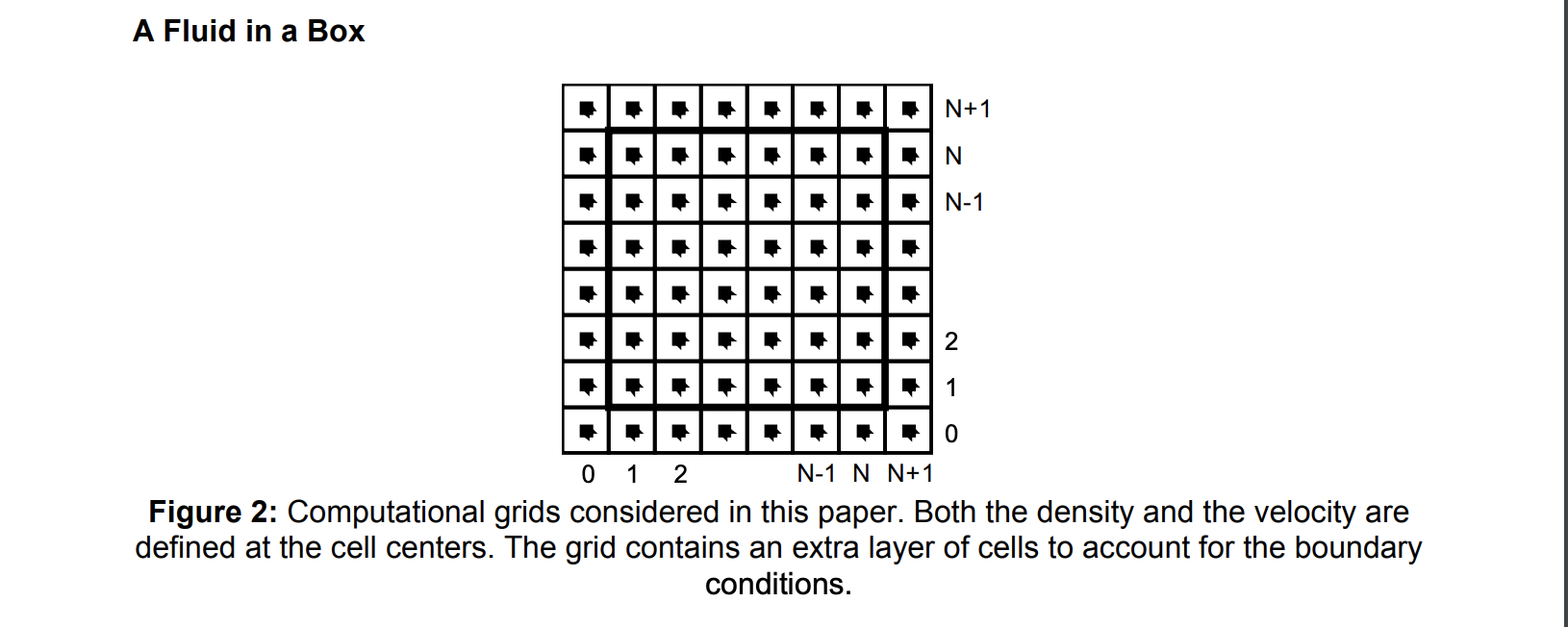
水面を格子に分割し、それぞれに密度と速度ベクトル(x方向分とy方向分)をもっています。太い線の部分が壁、境界(boundary)です。
実装に関して
実装に関しては以下のStable Fluid論文をベースに実装が説明された「Real-Time Fluid Dynamics for Games」が参考になります。
https://pdfs.semanticscholar.org/847f/819a4ea14bd789aca8bc88e85e906cfc657c.pdf
・Stable Fluids
Jos Stam氏がSIGGRAPH(アメリカコンピュータ学会におけるコンピュータグラフィックスを扱う分科会)1999年に発表された論文
https://d2f99xq7vri1nk.cloudfront.net/legacy_app_files/pdf/ns.pdf
その後にGameDevelopersConference2003にて「Real-Time Fluid Dynamics for Games」を発表されました。
資料のコードを見ながら実装するより、Github上にいくつかコードが存在しているので紹介します。
・Clang
・Python
・ JSに関しては以下のサイト
処理のフロー
Stable Fluidsより抜粋
外力: マウスで操作することにより力を与える(add_source)
↓
拡散(diffuse): 煙などの流体が周囲に広がる形で、なじんでいく様に移動していく現象
↓
移流(advect): 流体の速度差に着目して一定時間流れた後の速度を求める
毎フレーム以下のメソッド(速度、密度)を実行しています。
// 速度 2次元なのでu座標、v座標
void vel_step ( int N, float * u, float * v, float * u0, float * v0, float visc, float dt )
{
add_source ( N, u, u0, dt );
add_source ( N, v, v0, dt );
SWAP ( u0, u );
diffuse ( N, 1, u, u0, visc, dt );
SWAP ( v0, v );
diffuse ( N, 2, v, v0, visc, dt );
project ( N, u, v, u0, v0 );
SWAP ( u0, u ); SWAP ( v0, v );
advect ( N, 1, u, u0, u0, v0, dt );
advect ( N, 2, v, v0, u0, v0, dt );
project ( N, u, v, u0, v0 );
}
// 密度
void dens_step ( int N, float * x, float * x0, float * u, float * v, float diff, float dt )
{
add_source ( N, x, x0, dt );
SWAP ( x0, x );
diffuse ( N, 0, x, x0, diff, dt );
SWAP ( x0, x );
advect ( N, 0, x, x0, u, v, dt );
}
ここで出てくる、project(計画)メソッドに関して
一部のセルの流入が隣接セルの流入よりも高くまたは低くなることがあり、シミュレーションが完全に無秩序になる場合がある、それを防ぐために修正して平衡を維持しているとのこと。
ライブラリーの紹介
流体シミュレーションのライブラリーもGithubにいろいろ上がっているので、基本的なことを知った上で手を動かしつつ内部のコードを覗いてみるのもオススメです。
WebGLを用いたシュミレーション
GPGPUを駆使していたり、外力が色として反映されるようになっていたりと工夫されています。
自分はopenframeworksが好きなので以下を試してみました。
流体いいですね、心地よい動きです。
参考資料
いろいろ調べていて自分が気に入った資料をあげておきます。
・流体シミュレーションを使った自然現象の表現
・クリエイティブプログラミングのための三次元流体シミュレーションツールキットの研究
https://core.ac.uk/download/pdf/157813671.pdf
最後に
ふだん身の回りにある物を理論、数式をもとにプログラムを実装していくことで、私たちのいる世界が実に複雑なシステムで成り立っているのが実感できるのではないでしょうか。そして、私たちが普段感じる心地よいと思える「川の流れ」、「風の流れ」を観察することによって、よりよいユーザーエクスペリエンスを提供していきたいと思います。最後まで見てくださってありがとうございます。